Curvature of the Universe
The galaxies spread throughout the universe are
moving away from each other. To describe this
mathematically, cosmologists use a universal scale factor called
a(t) which grows as the universe expands, along with a
coordinate system that expands along with the galaxies. In
this coordinate system, called co-moving coordinates, the galaxy
positions do not change.
Said another way, the position of some far away galaxy with respect to our galaxy is given by the vector R(t). We write this vector as
R(t) = a(t) · X
where we have factored all of the time
dependence of R(t) into a(t), leaving the vector X
with no time dependence, representing the co-moving distance
between the two galaxies. The common convention is to
set a(t) = 1 at the current age of the universe, such that
the physical vector R(t) is equal to the co-moving
vector X today.
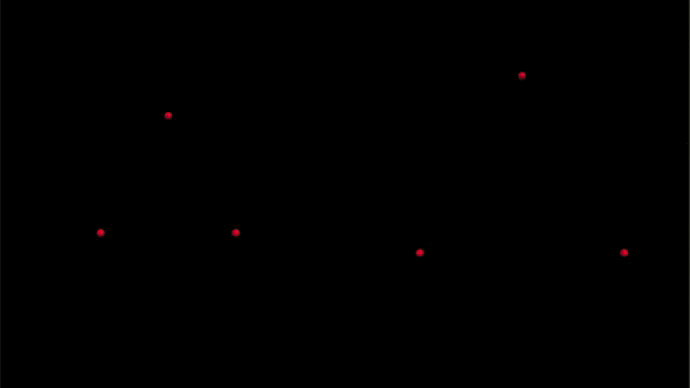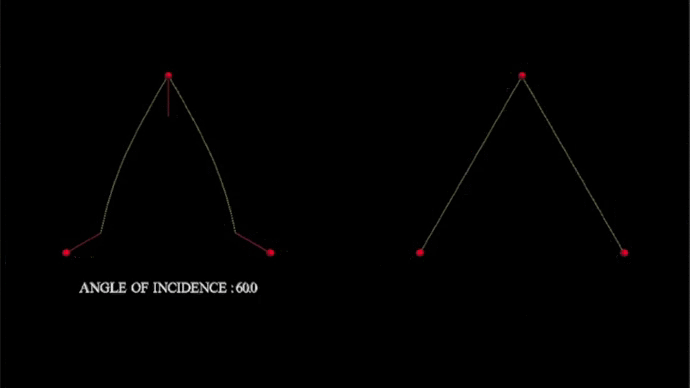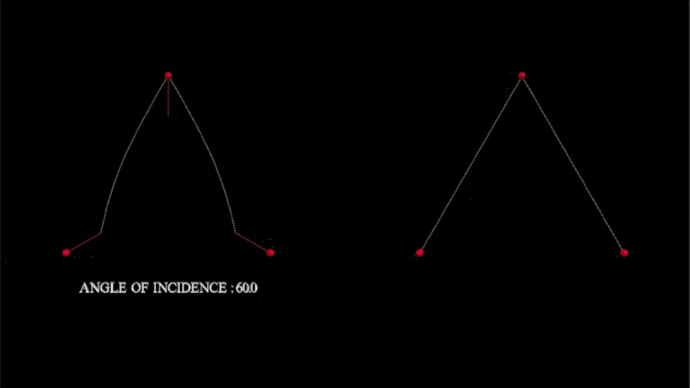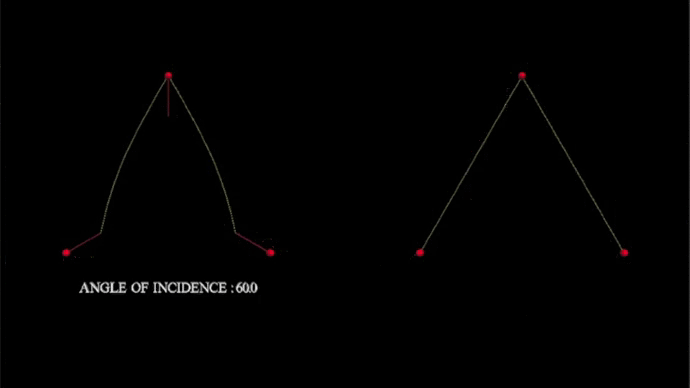
The history and ultimate fate of the expansion is described by the function a(t). If the universe contained a lot of dark matter, called a closed universe, a(t) would rise, reach a maximum, and then fall. The universe would suffer a "Big Crunch" in which the galaxies would all collide at some point in the future. If the universe contained very little dark matter, called an open universe, a(t) would rise forever. Galaxies would forever be moving away from each other, with expansion never stopping. If the universe contained precisely the critical density of matter and energy, called a flat universe, a(t) would rise forever but would approach an asymptote at some final value. Galaxies would still be forever moving away from each other, but the expansion of the universe would approach zero. The following plot shows these cases.
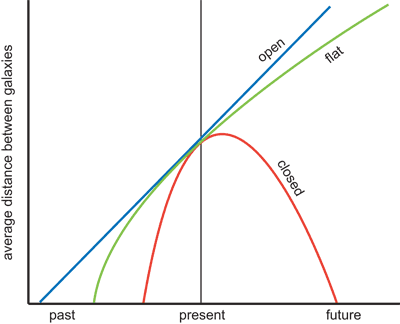
The history and ultimate fate of the expansion is described by the function a(t). If the universe contained a lot of dark matter, called a closed universe, a(t) would rise, reach a maximum, and then fall. The universe would suffer a "Big Crunch" in which the galaxies would all collide at some point in the future. If the universe contained very little dark matter, called an open universe, a(t) would rise forever. Galaxies would forever be moving away from each other, with expansion never stopping. If the universe contained precisely the critical density of matter and energy, called a flat universe, a(t) would rise forever but would approach an asymptote at some final value. Galaxies would still be forever moving away from each other, but the expansion of the universe would approach zero. The following plot shows these cases.